Buy this illustration Proven Cone by elkement on canvas, ArtFrame, poster and wallpaper, printed on demand in high quality.
About "Proven Cone"
by elkement
About the artwork
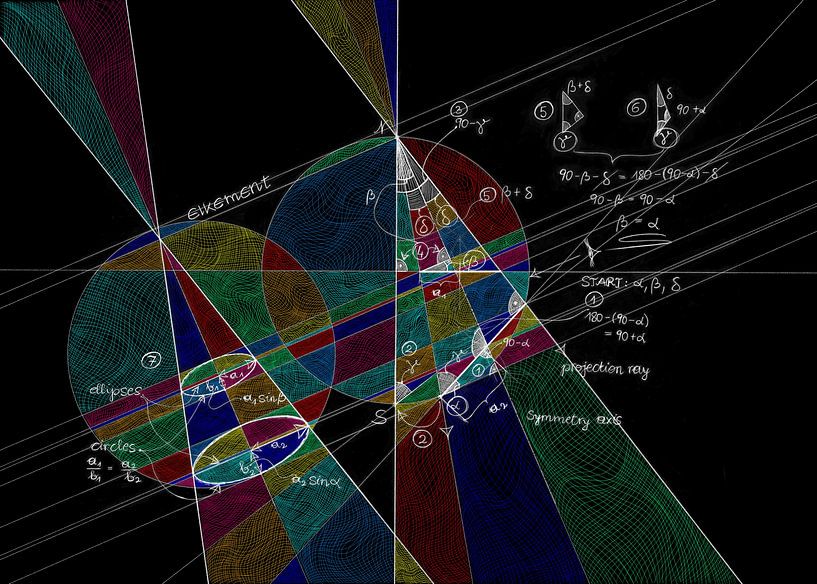
A digitally enhanced mathematical proof originally drawn on paper: Why circles are projected onto circles stereographically.
The circle on the sphere and its image in the equatorial plane are both connected by some sort of cone. If the circle would be the base of the cone, the intersection with a plane would be an ellipse. As the intersection is a circle, the base must be an ellipse. I am looking at this cone, from a direction perpendicular to the cone's axis. The actual proof that circles are projected onto circles is carried out by spotting various triangles and angles in this sketch.
I have drawn it in 2021 when I was not yet sure if it should be just a proof or also art. In 2024 I have been sure it should be both! I want to prove (:-)) that also "sparse mathematics" can be beautiful.
Created on paper, scanned and inverted, digital overlay created with Procreate. No AI!

About elkement
Elke Stangl (elkement) (she/her) is an Austrian physics PhD working as an engineer. Her mathematical art is borne out of her life-long passion for the theoretical underpinnings of her craft. She is creating virtual three-dimensional structures from mathematical functions – digitally with code or with ruler and compass, using.. Read more…
 Germany
Germany Ordered in November 2020
Ordered in November 2020
 Netherlands
Netherlands Ordered in November 2023
Ordered in November 2023
 Germany
Germany Ordered in July 2019
Ordered in July 2019
 Germany
Germany Ordered in October 2019
Ordered in October 2019
 Netherlands
Netherlands Ordered in November 2020
Ordered in November 2020
 Germany
Germany Ordered in November 2020
Ordered in November 2020
 Germany
Germany Ordered in January 2020
Ordered in January 2020
 Germany
Germany Ordered in March 2024
Ordered in March 2024
 Netherlands
Netherlands Ordered in December 2018
Ordered in December 2018

 Netherlands
Netherlands Ordered in May 2021
Ordered in May 2021
 Netherlands
Netherlands Ordered in August 2018
Ordered in August 2018

 Germany
Germany Ordered in March 2019
Ordered in March 2019
About the material
ArtFrame™
Interchangeable Art Prints
- High-quality print
- Easily interchangeable
- Acoustic function
- Large sizes available
Discover the artworks of elkement
 Peek through the Peakselkement
Peek through the Peakselkement Stellar Coronaelkement
Stellar Coronaelkement After the Encounterelkement
After the Encounterelkement Double Star Gateelkement
Double Star Gateelkement Patented Mouseelkement
Patented Mouseelkement Reality and Imagination #12elkement
Reality and Imagination #12elkement Reality and Imagination #2elkement
Reality and Imagination #2elkement Diffracted Surge in the Negativeelkement
Diffracted Surge in the Negativeelkement Lissajous Quadrupoleelkement
Lissajous Quadrupoleelkement Inverted Atollelkement
Inverted Atollelkement Echo of the Double Star Gateelkement
Echo of the Double Star Gateelkement Peek through the Echoed Peakselkement
Peek through the Echoed Peakselkement Lissajous, Orthographic: Three Four Fiveelkement
Lissajous, Orthographic: Three Four Fiveelkement Frozen Harmonicselkement
Frozen Harmonicselkement Clovery Coppery Citadelelkement
Clovery Coppery Citadelelkement Tornado on Tatooineelkement
Tornado on Tatooineelkement Cathedral of Mathelkement
Cathedral of Mathelkement Celebration of Diffractionelkement
Celebration of Diffractionelkement Orbital Summerelkement
Orbital Summerelkement Circles to Circles #3elkement
Circles to Circles #3elkement












 Geometric
Geometric Illustrations
Illustrations Vibrant Colors
Vibrant Colors









