Buy this flower art Peano dahlias by Tis Veugen on canvas, ArtFrame, poster and wallpaper, printed on demand in high quality.
About "Peano dahlias"
by Tis Veugen
About the artwork
The Peano curve is the first example of a space-filling curve, discovered by Giuseppe Peano in 1890. A line is drawn recursively through a 3x3 grid of squares from top left to bottom right (in our picture). On each iteration, a square is replaced by a smaller 3x3 grid, etc. In the original curve, a line only looks like a Z, or its horizontally/vertically mirrored version. (There are 8 ways due to rotation and flipping.) The Z can also be flipped diagonally, creating an upside-down N. In each of the 9 basic squares a choice can be made between Z and N. Of the 2^9 = 512 variants I choose the symmetrical one: ZNNNZNNNZ. Each square of the tessellation (without tiling deformations) is renderered with 4 half-flowers and a stem that follows the path of the Peano curve. So I made twelve square images to create the entire tessellation.

About Tis Veugen
My training as a mathematician and my experience as a software programmer are the basic elements for designing my works of art. Since my retirement in 2019 I have started creating digital art with a mathematical slant. The works of M.C. Escher are a source of inspiration. Thanks to programs.. Read more…
 Netherlands
Netherlands Ordered in June 2022
Ordered in June 2022
 Netherlands
Netherlands Ordered in December 2024
Ordered in December 2024
 Germany
Germany Ordered in April 2020
Ordered in April 2020
 Germany
Germany Ordered in April 2020
Ordered in April 2020
 Netherlands
Netherlands Ordered in November 2024
Ordered in November 2024
 Netherlands
Netherlands Ordered in April 2017
Ordered in April 2017
 Germany
Germany Ordered in January 2021
Ordered in January 2021
 Netherlands
Netherlands Ordered in April 2020
Ordered in April 2020
 Germany
Germany Ordered in June 2020
Ordered in June 2020
 Netherlands
Netherlands Ordered in April 2021
Ordered in April 2021
 Germany
Germany Ordered in February 2023
Ordered in February 2023
 Germany
Germany Ordered in August 2023
Ordered in August 2023
About the material
Poster
Fine-art quality posters for your wall
- High-quality photographic prints
- Thick and durable photo paper
- Use your own frame
- Optional white border
Discover the artworks of Tis Veugen
 BlossomTis Veugen
BlossomTis Veugen Fish Sphere SurfaceTis Veugen
Fish Sphere SurfaceTis Veugen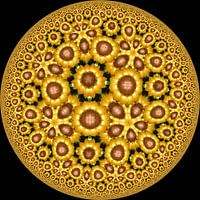 Glow SunflowersTis Veugen
Glow SunflowersTis Veugen Dance of ParrotsTis Veugen
Dance of ParrotsTis Veugen Seagull RhododendronTis Veugen
Seagull RhododendronTis Veugen Square ButterfliesTis Veugen
Square ButterfliesTis Veugen Triple Spiral of Four FishTis Veugen
Triple Spiral of Four FishTis Veugen Trio Spiral of Sunflowers IITis Veugen
Trio Spiral of Sunflowers IITis Veugen Double Spiral of Tropical FishTis Veugen
Double Spiral of Tropical FishTis Veugen Hyperbolic LizardsTis Veugen
Hyperbolic LizardsTis Veugen Square Hyperbolic LizardsTis Veugen
Square Hyperbolic LizardsTis Veugen Dahlia sunflowersTis Veugen
Dahlia sunflowersTis Veugen Swan Square LimitTis Veugen
Swan Square LimitTis Veugen B/W Swans Octagon LimitTis Veugen
B/W Swans Octagon LimitTis Veugen B/W Swans Square FractalTis Veugen
B/W Swans Square FractalTis Veugen Swans Square Fractal OctagonTis Veugen
Swans Square Fractal OctagonTis Veugen Hilbert birdsTis Veugen
Hilbert birdsTis Veugen Peano dahliasTis Veugen
Peano dahliasTis Veugen Meander Peano FishTis Veugen
Meander Peano FishTis Veugen Gosper-13 birdsTis Veugen
Gosper-13 birdsTis Veugen













 Countries & Travel
Countries & Travel Dahlia
Dahlia Digital art
Digital art Flowers
Flowers Fractal
Fractal Geometric
Geometric Joyful Moments
Joyful Moments Modern shapes and lines
Modern shapes and lines Nature and weather
Nature and weather Optical illusions
Optical illusions Patterns
Patterns Symmetry
Symmetry Vibrant Colors
Vibrant Colors Whimsical Wonders
Whimsical Wonders









